O volume do sólido limitado inferiormente pelo plano z = 10 e limitado superiormente pelo paraboloide z = 2 (x2 y2) é?B F x y z x 2 z y 2 z encerrada por el paraboloide z 1 x 2 y 2 y el plano z cF from FINANCIAL 3 at Strayer UniversityI) La regi´on de integraci´on es el interior del paraboloide limitado por el plano z = 2 x y z Como la proyecci´on de dicha regi´on sobre el plano z = 0 es el c´ırculo C x2 y2 ≤ 4, la integral triple se puede descomponer entonces como I = ZZ C dxdy Z 2 (x2y2)/2 (x2 y2)dz Al escribir la integral en coordenadas cil´ındricas, se
What Is The Surface Area Of The Portion Of The Paraboloid Z 4 𝑥 2 𝑦 2 That Lies Above The Xy Plane Quora
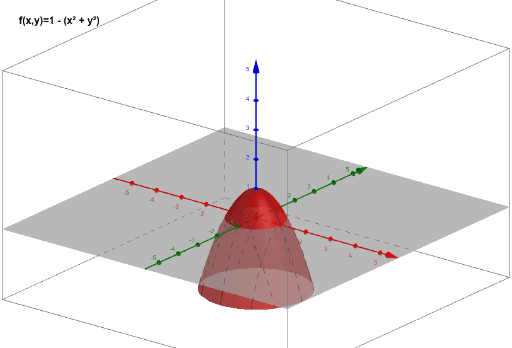
Graph of paraboloid z=1-x^2-y^2
Graph of paraboloid z=1-x^2-y^2-C alculo vectorial Sesi on 8 Integrales de Super cie IdS de campo escalar sobre una super cie de nida expl citamente Sea Suna super cie correspondiente al gr a co de la funci on C1, z= g(x;y) de DˆR2 en R, y fun campo escalar continuo cuyo dominio (en R3) incluye a S La integral de super cie del campo escalar fsobre la super cie S, se anota y de neCalcule a integral de superfície ∬ S F ⋅ dS para o campo vetorial F e superfície orientada S dados abaixo Em outras palavras, determine o fluxo de F através de S Para superfícies fechadas, use a orientação positiva (para fora) F(x, y, z) = (x y)i zj xzk




Solved Find The Area Of The Surface The Part Of
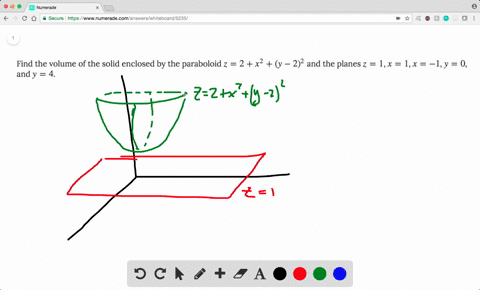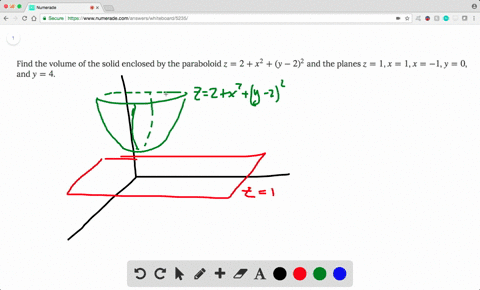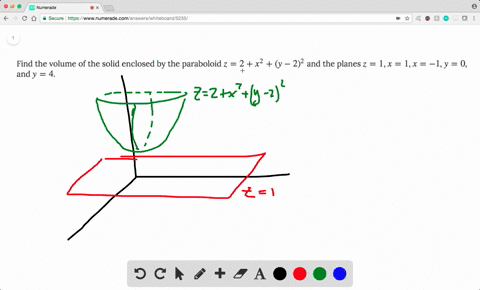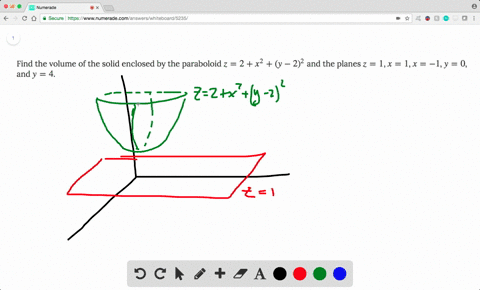
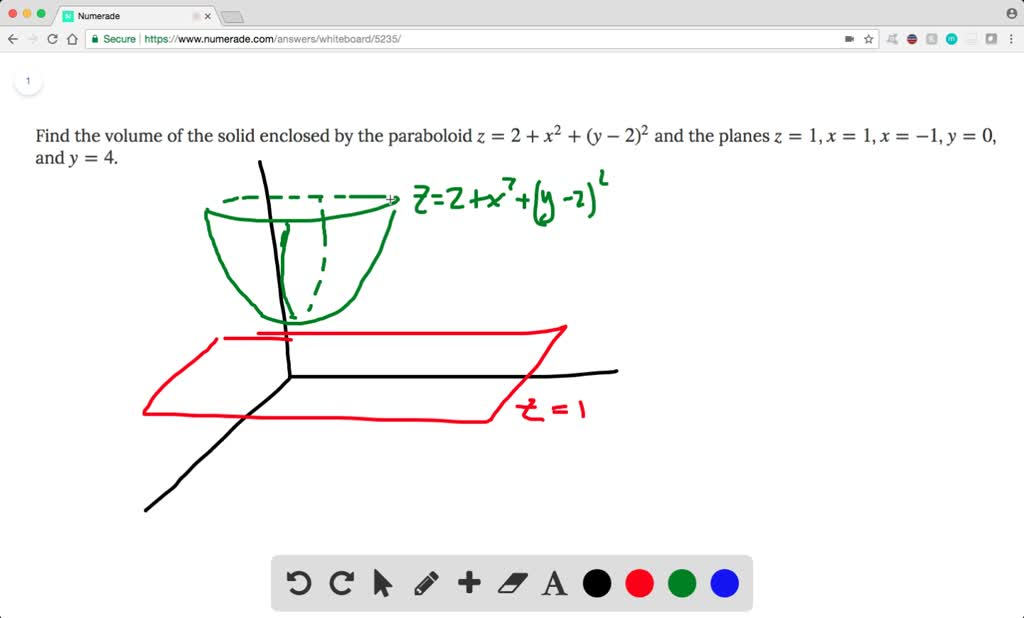
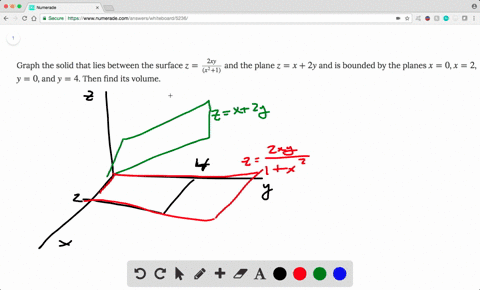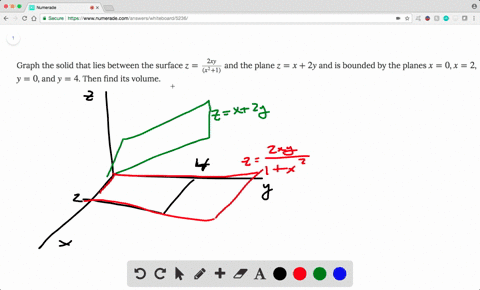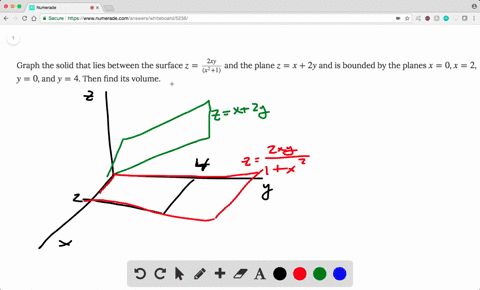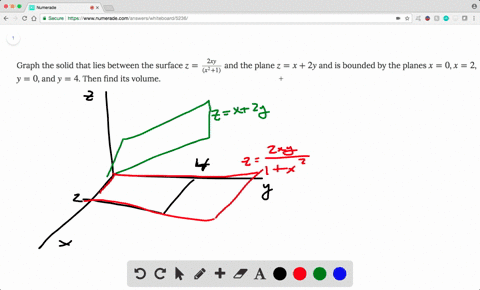
Boloide z= 1 x2 y2 La intersección del plano con el paraboloide es la circunferencia x2y2 = 1 contenida en el plano z= 0 El volumen pedido es V = Z Z D 1 x2 y2 dxdy siendo Del disco D = f(x;y;0) x2 y2 1g Pasando a coordenadas polares, se obtiene V = Z Z D 1 x2 y2 dxdy= Z Z D0 (1 r)rdrd siendo D0= 0;1 0;2ˇ el transformado del recinto Den coordenadas polaresF)dV = ZZZ E dV = 4 Z ˇ=2 0 Z 1 0 Z r2 0 rdzdrd = ˇ 2 (96) Luego (95) y (96) comprueban (93) para el campo vectorial y solido de1(1, se˘c~ao 152) Encontre o volume do s olido delimitado pelo paraboloide z= 2 x2 (y 2)2 e pelos planos z= 1, x= 1, x= 1, y= 0 e y= 4 Solu˘c~ao Observe que o s olido Eest a abaixo da superf cie z= 2x2(y 2)2 e acima do ret^angulo 1;1 0;4 em z= 1 (ver gura abaixo) Algebricamente,
24 Hallar el volumen del s olido acotado superiormente por el paraboloide z = 5 x2 y2, e inferiormente por el paraboloide z = 4x2 4y2 Hallar tambi en su masa y su centro de gravedad siendo la densidad en cada punto m(x;y;z) = 8 z 25 Se considera el s olido interior al cilindro x2 y2 = 1, limitado superiormente por laO paraboloide z =x2 y2 se converte em z =r2 e o cilindro x2 y2 =4se converte em r2 =4 ou r = 2 Observemos que a projec¸˜ao de W sobre o plano xy ´e o disco Dxy x2 y2 ≤ 4 Como as varia¸c˜oes de r e θ s˜ao determinadas na projec¸˜ao Dxy, ent˜ao 0≤ r ≤ 2 e 0 ≤ θ ≤ 2π54 Volume de um sólido Nesta seção damos o volume de um sólido em várias formas, utilizando sistema cartesiano, coordenadas polares, coordenadas cilíndricas, coordenadas esféricas, volume de um sólido de revolução, etc
Problemasresueltos Solución Lainterseccióndelasuperficieconelplanoxy es z = x2 ¡y2 z = 0!Bol exámenes int sup grado ingeniería integrales de superficie, th de stokes gauss sea la región del espacio comprendida entre el paraboloide y2 el plano sea elAmanda Silva Determine a área da superfície S, onde S ´e a parte do paraboloide z = x 2 y^2 cortada pelo plano z = 3
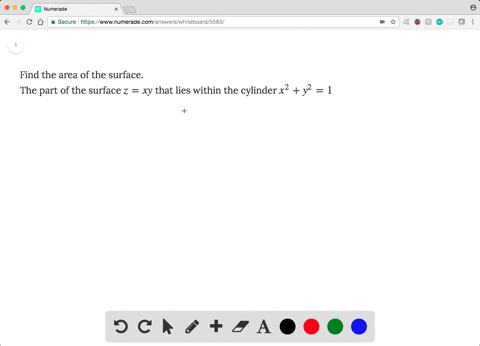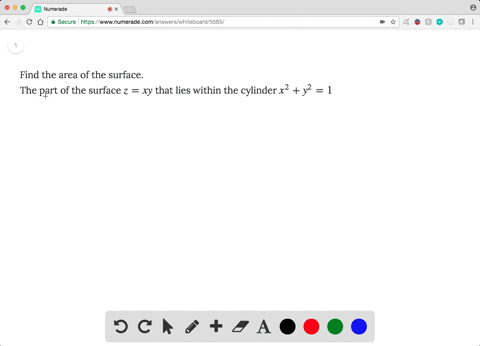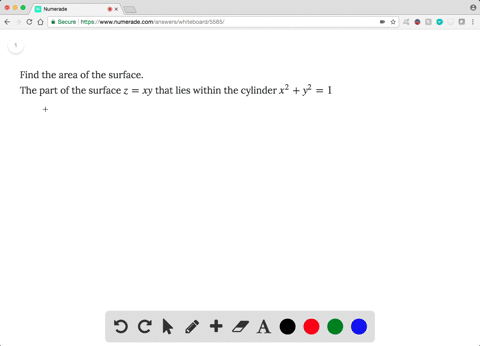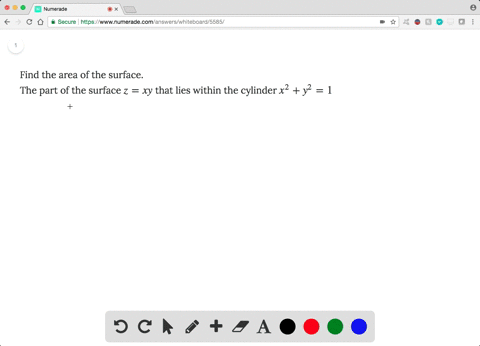



Solved Find The Area Of The Surface The Part Of



Solved Find The Volume Of The Solid Enclosed By T
Esercizi di calcolo vettoriale integrale Esercizio 1 Sia G = {(x,y,z) ∈ R3 x2 y2 ≤ 1, 0 ≤ z ≤ 2− p x2 y2} (1) Disegnare G e verificare che la frontiera di G siGráficos de algumas superfícies < Parabolóide hiperbólico z = x2 y2 < Parabolóide de revolução z = x2 y2 < Hiperbolóide de uma folha x2 y2 z2 = 1 < Hiperbolóide de duas folhas x2 y2 z2 = 1Cálculo Cálculo Volume 2 5ª Edição James Stewart 166 39 Determine a área da superfície A parte do paraboloide hiperbólico z = y 2 x 2 que está entre os cilindros x 2 y 2 = 1 e



Http Webpages Fc Ul Pt Jaruiz Multivariable Calculus Excerptsmath23b Pdf
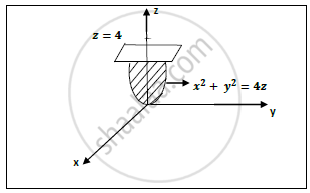



Find The Volume Of The Paraboloid X 2 Y 2 4 Z Cut Off By The Plane 𝒛 𝟒 Applied Mathematics 2 Shaalaa Com
paraboloide z=1x2y2 Publicado por tartari ( 2 intervenciones) el Gracias por contestarme, pues ya lo estaba haciendo así, pero no se porque razon la version de matlab que estoy utilizando no me muestra la grafica ni nada Además tambien debo realizar a continuacion las siguientes cosas Utilizando una parametrizacion con21 Debajo de la superficie z=xy y arriba del tríangulo con vértices (1,1), (4,1)y (1,2) 22 Emcerrado por el paraboloide z=x^23y^2 y los planos x=0, y=1, y=x, z=0 23 Acotado por los planos coordenados y el plano 3x2yz=6 24 acotado por los planos z=x,y=x, xy=2 y z=0 25Let S be part of the paraboloid z = 1 x^2 y^2 where z >= 0 This is a surface Define the orientation to be outward Now compute the integral double integral_S y dy dz z dz dx x dx dy This integral is basically the same as an integral over the surface S




Volumen De Un Paraboloide Geogebra




Find The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Study Com
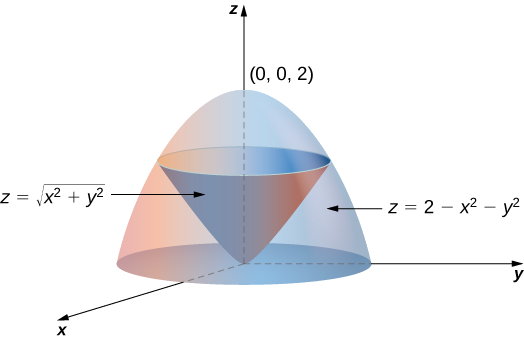
A superfície azul é o paraboloide (virado para cima porque temos e multiplicados por termos positivos), e a vermelha, a folha superior do cone (pois não podemos ter raiz negativa) Como podemos ver, no plano , temos um domínio Em , o sólido é limitado embaixo pelo paraboloide e2 3 4 5 6 168 Exercícios Um hemisfério H e um pedaço P de um parabolóide estäo mostrados Suponha que F seja um campo vetorial sobre RSAnswer to Let S be the paraboloid z = 1 (x^2 y^2), z greater than or equal to 0, oriented upward and deronS be the boundary of S with its
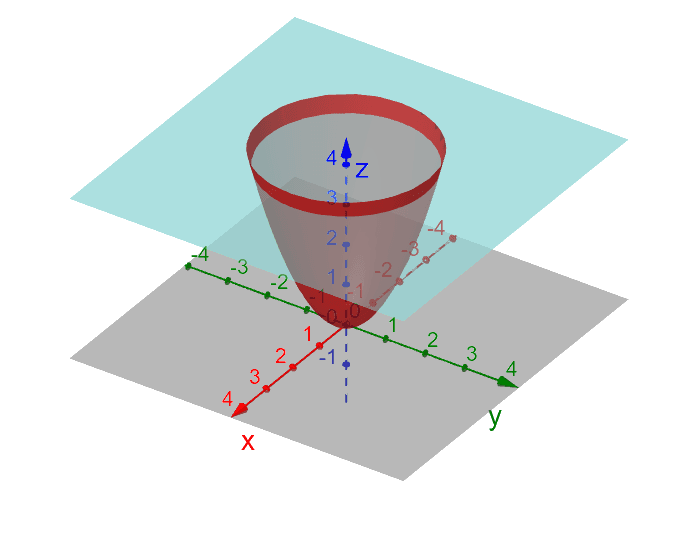



Paraboloide Z X Y E Plano Z 4 Geogebra
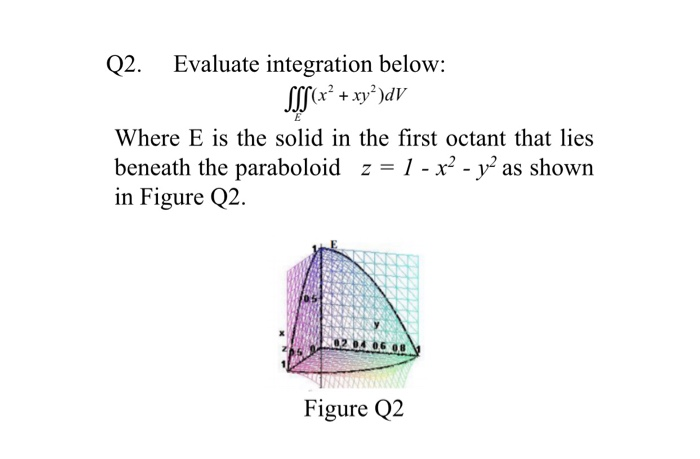



Q2 Evaluate Integration Below Sss R Xy Dv Where Chegg Com
UFSC CALCULO 3 133 1A PROVA (SOLUC˘ AO)~ RAPHAEL DA HORA (1) Calcule, mudando a ordem de integrac~ao, Z 1 0 Z 1 p x ey3dydx Solu˘c~ao Vemos que a regi~ao por ser descrita por 0 y 1, 0 x y2Portanto podemos reescrever a integralAbaixo do paraboloide z = x2 y2 e que se encontra dentro do cilindro x 2 y = 2xe fora do cilindro x2 y = 1 Solu˘c~ao Temos que 0 z x2 y2 Como o s olido se encontra dentro do cilindro x2 y 2= 2xe fora do cilindro x2 y = 1, devemos fazer a interse˘c~ao desses dois cilindros, isto e, ˆ x 2 y = 2x x 2 y = 1)2x= 1 ,x= 1 2Answer to A solid is bounded below the paraboloid z = 1 x^{2} y^{2} and above by the xy plane Compute the volume of the solid using polar




Volumen De Un Solido Limitado Por El Paraboloide Y Un Plano Youtube



A Paraboloid Described By Z X 2 Y 2 On The Xy Plane And Partly Inside The Cylinder X 2 Y 2 2y How
Example Find the volume of the solid D bounded by the paraboloid S z = 25−x2 −y2 and the xyplane Solution The paraboloid S z = 25 − x2 − y2 intersect the xyplane p z = 0 in the curve C 0 = 25−x2 −y2, which is a circle x2 y2 = 52 So the shadow R of the solid D after projecting onto xyplane is given by the circular disc R = {(x,y) x2 y2 ≤ 52}, in polar coordinates isF(x,y)=xy, PARABOLOIDE IPERBOLICO, rigata Questa funzione si chiama rigata perche' le sezioni con piani paralleli ai piani xz e yz sono rette Essa interseca il piano xy lungo gliassi525 0 25 5 x2 2 0 y 0 25 5 75 10 z25 f(x,y)=c x2 a2 y2 b2 CONO con a = 1 2,b= 1 3,c=1 Se a = b esso si ottiene dalla rotazione della curva z = c by del piano yz attorno all'asse z 51Problema 1 Hallar el área de la porción de la superficie S z=x2(y 1)2comprendida entre los planos z=1, z=4 Solución p 6 17 p 17 5 p 5 RESOLUCIÓN Podemos parametrizar S (Figura1) mediante r(x;y)=(x;y;x2(y 1)2) ((x;y)2D), donde D= (x;y)2R2 1 x2(y 1)2 4 Figura 1
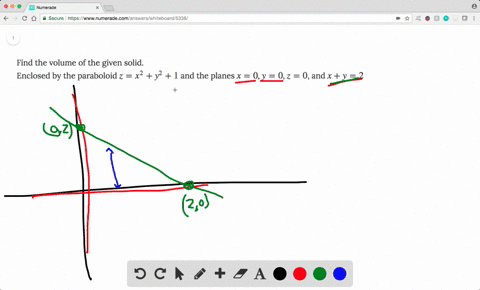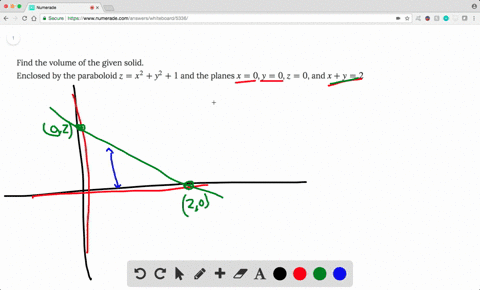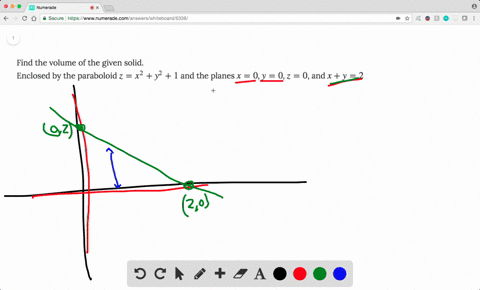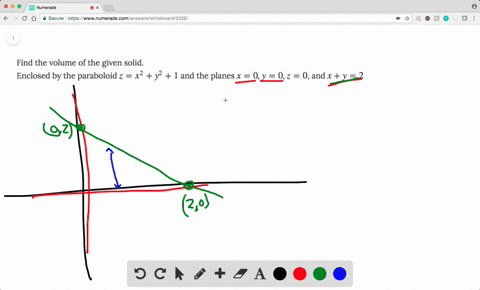



Solved Find The Volume Of The Solid Lying Under T




Draw The Solid Bounded By The Paraboloid Z 6 X 2 Y 2 And The Plane Z 0 Study Com
The 2 given surfaces are reflections of each other at the plane y=z because each of them mapped onto the other by interchanging between y and z Therefore their intersection contained inside that plane, and it is the curve given by Hence the per1 Calcule el área de la porción del paraboloide z = x2 y2 que está comprendidaentrelosplanosz = 0 yz = 1 Solución La intersección del paraboloide con el plano z = 0 es el punto (0;0) y con el plano z = 1 es la circunferencia x2 y2 = 1 La región limitada por la proyeccióndedichacircunferenciasobreelplanoXY es D = ' (x;y) 2 R2 x2 y2 • 1 "MAT 2352 CÁLC PARA FUNÇÕES DE VÁRIAS VAR II 2o SEMESTRE 14 LISTA 3 1 Calcule as integrais abaixo, esboçando o domínio de integração (a) RR B R xyzdxdydz, onde B é o paralelepípedo 0 x 2, 0 y 1, e 1 z 2
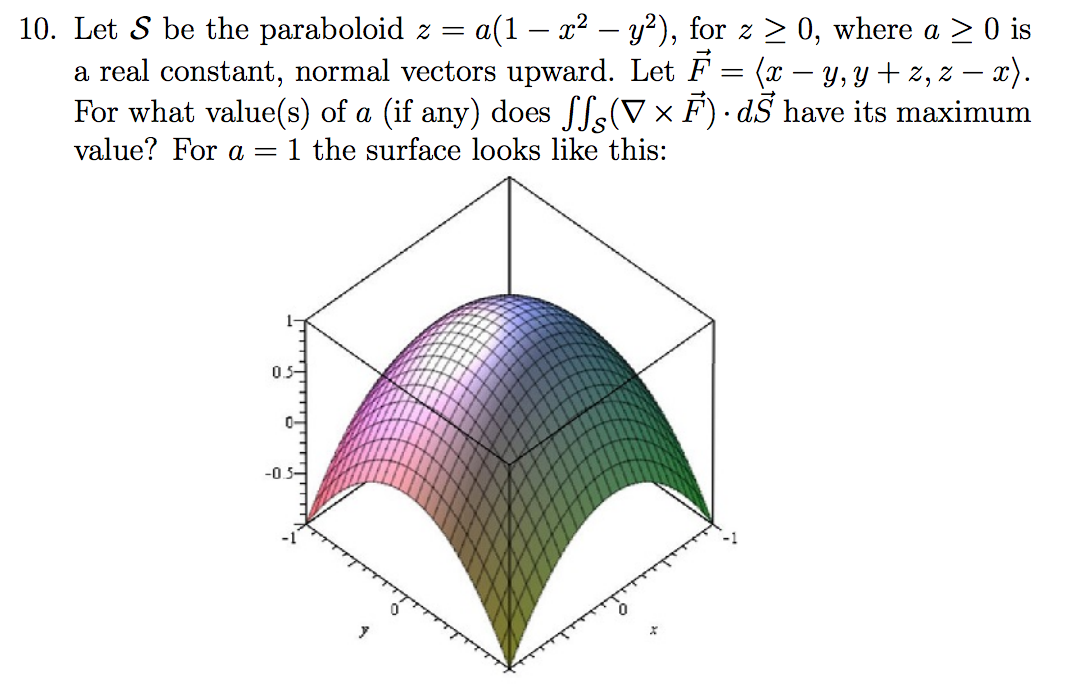



Let S Be The Paraboloid Z A 1 X 2 Y 2 For Z Chegg Com




Example 2 Find The Volume Of The Solid Bounded By The Chegg Com
See the answer For the vector field F= and the surface which is the part of the paraboloide z=1x^2y^2 that is above the plane z=0 cerify Stokes theoremCalculo Multivariable Larson 500qxd 9/15/05 330 PM Page 297 5 z y Funciones de varias x variables z y Las áreas mostradas en el mapa climático mundial representan el rango de temperatura anual normal de las regiones en la Tierra ¿Cuáles son las dos características geográficas que tienen mayor x efecto en el rango de temperatura?1)Determine o volume do s olido abaixo do paraboloide z = x2 y2 e acima da regi~ao limitada por y = x2 e x = y2 2)Calcule as integrais trocando a ordem de integra˘c~ao a) Z 1 0 Z 3 3y ex2dxdy b) Z 3 0 Z 9 y2 y cos(x2)dxdy 3)Calcule a integral ZZ D p 1 x2 y2dA, onde D e a regi~ao do plano de nida por x2 y2 1 Indenti que a integral como



Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




Solved Find The Area Of The Surface The Part Of
Sólida E delimitada pelo paraboloide z = 1 — x2 — _y2e pelo plano Z = O SOLUÇÃO A superficie S é constituída pela superficie parabólica do topo, 91 , e pela superficie circular do fundo, Sr (veja a Figura 12) Como S é uma superficie fechada, usamos a conDetermine a área da parte do paraboloide z = x2 y2 que está abaixo do plano z = 9 Resposta A área da superfície do paraboloide, usando coordenadas polares, é A(S) = ZZ D q 1 (2x)2 (2y)2dA = Z 2ˇ 0 Z 3 0 r p 1 4r2drd = ˇ 6 (37 p 37 1)Ejercicios Resueltos de Cálculo III Ejercicios Resueltos de Cálculo III 1 Considere y a) Demuestre que las rectas dadas se cortan Encuentre el punto de intersección Solución b) Encuentre una ecuación del plano que contiene a esas rectas Solución Como las rectas de cortan resulta que determinan un plano
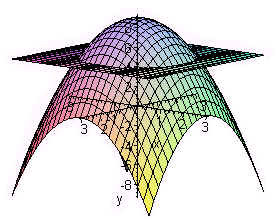



Math 2 Midterm 2




X X2 Y2 Z2 Y X2 Y2 Z2 Z X2 Y2 Z2 Brainly In
Como você encontra a área de superfície da parte do parabolóide circular # z = x ^ 2 y ^ 2 # que fica dentro do cilindro # x ^ 2 y ^ 2 = 1 #?Plano z = 4 e acima do paraboloide z = 1 x2 y2 A densidade em qualquer ponto é proporcional à distância do ponto ao eixo do cilindro Determine a massa de E Resposta A massa é m = ZZZ E K q x2 y2dV = Z 2ˇ 0 Z 1 0 Z 4 1 r2 (Kr)rdzdrd = 12ˇK 5 Hallar el volumen del sólido limitado por el plano z=0 y el paraboloide z=1(x^2y^2) Podemos cambiar con el deslizador k el valor y se puede ver como cambia el paraboloide , en el ejemplo realizamos los cálculos para k=1




How To Find The Volume Of A Solid Region Bounded By Paraboloid Z 4 X 2 2y 2 And The Xy Plane Quora



Search Q Z 3dsqrt X 5e2 2by 5e2 Tbm Isch
S = ˇ 2 (95) Ahora bien, ZZZ E div(!Question For The Vector Field F= And The Surface Which Is The Part Of The Paraboloide Z=1x^2y^2 That Is Above The Plane Z=0 Cerify Stokes Theorem This problem has been solved! Finding the surface area of the paraboloid $z = 1 x^2 y^2$ that lies above the plane $z = 4$



Triple Integrals In Cylindrical And Spherical Coordinates




Triple Integral In Cylindrical Coordinates Plan And Example Parabaloid And Plane Bounds Youtube
Universidade Federal do Rio de Janeiro Instituto de Matem¶atica Departamento de M¶etodos Matem¶aticos Lista 6 C¶alculo III 08/01 Integral de Superf¶‡cie Escalar e Area, com Parametriza»c~ao de Superf¶‡cies¶Bol examenees triples grado ingeniería integrales triples calcula el volumen del sólido acotado superiormente por el paraboloide x2 y2 el plano (avelinoY = x y = ¡x yconlosplanos x = 1 y x = 3;



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




Find The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Unit Circle In The Xy Plane Study Com
La regi on s olida encerrada por el paraboloide z= 1 x2 y2 y el plano z= 0 Desarrollo En la actividad 6 del tema sobre integrales de super cies se veri c o que ZZ S!INTEGRACIÓN MÚLTIPLE INTEGRALES TRIPLES 1/18 1Problema 1 Calcular ZZZ T zdxdydz; Volumen de un paraboloide Hallar el volumen del sólido limitado por el plano z=0 y el paraboloide z=1 (x^2y^2) Podemos cambiar con el deslizador k el valor y se puede ver como cambia el paraboloide, en el ejemplo realizamos los cálculos para k=1 Solución Si ponemos z=0 en la ecuación del paraboloide, obtenemos x^2y^2=1Esto significa



What Is The Surface Area Of The Portion Of The Paraboloid Z 4 𝑥 2 𝑦 2 That Lies Above The Xy Plane Quora



Volume Of A Solid With A Known Cross Section
Elimine os parâmetros para mostrar que a superfície é um paraboloide elíptico e escreva outra integral dupla que forneça sua área ver resposta $\displaystyle \int^{2\pi}_{0}\int_{0}^{2} \sqrt{4b^2 u^4 \cos^{2}v 4a^2 u^4 \sin^{2} v a^2 b^2 u^2} dudv$Siendo T el dominio del primer octante delimitado por las superficies y2 z=1, x2 z=1 Solución 1 6 RESOLUCIÓNLa intersección de ambas superficies en el primer octante se



Find The Point On The Paraboloid Z X 2 Y 2 Which Is Closest To The Point 3 6 4 Sarthaks Econnect Largest Online Education Community




Tarea Semana 14 Sesion 1 1




Hyperbolic Paraboloid Surface Z Y 2 X 2 Download Scientific Diagram




Calcular El Volumen Del Solido Acotado Por El Paraboloide Z 9 X 2 Y 2 Y El Plano Z 0 Youtube




Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 In Rectangular Coordinates Study Com




Calculus Volume Integral Mathematics Stack Exchange
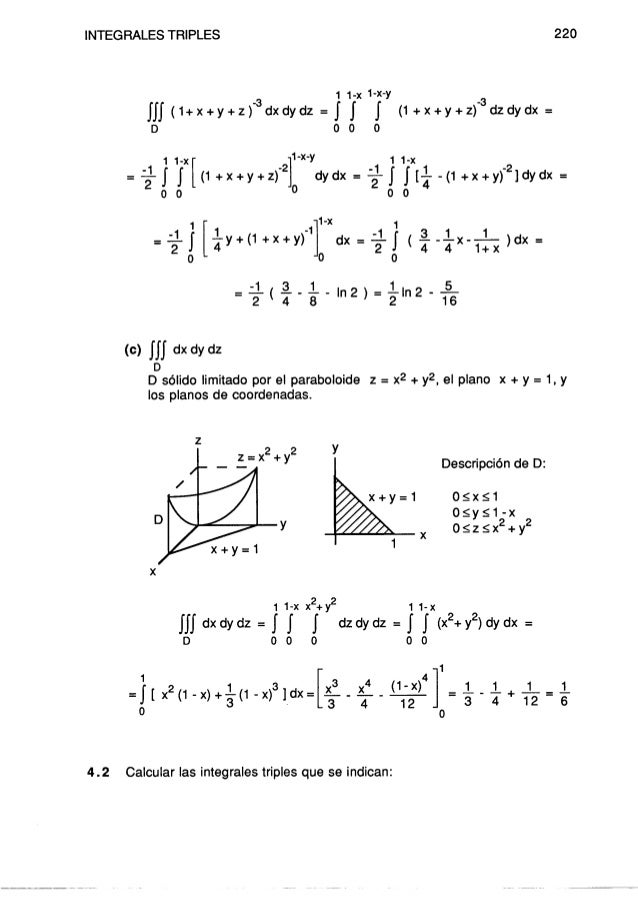



Integrales Triples
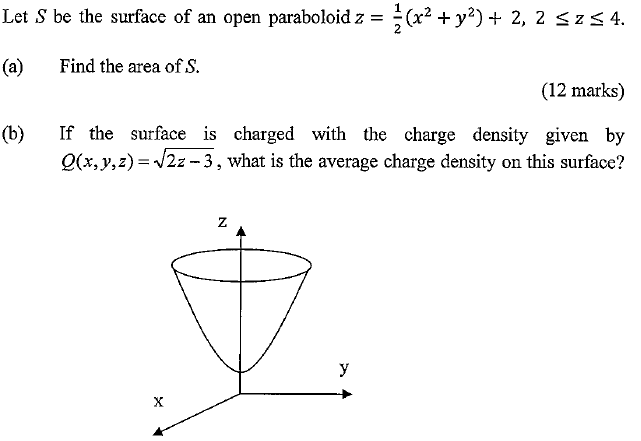



Let S Be The Surface Of An Open Paraboloid Z Chegg Com




Example 4 Find The Volume Of The Solid That Lies Chegg Com




Surfaces Part 2




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange



Www Ualberta Ca Rjia Math215 Hwks Sol8 Pdf




Solved A Solid G Is Bounded Above By The Paraboloid Z 1 Chegg Com




1 Double Integrals Cankaya Universitesi Flip Ebook Pages 1 16 Anyflip Anyflip




Calcular El Volumen De Un Paraboloide X 2 Y 2 1 Z 10



What Is The Volume Between Paraboloid Z X 2 Y 2 And Y X 2 Z 2 Quora
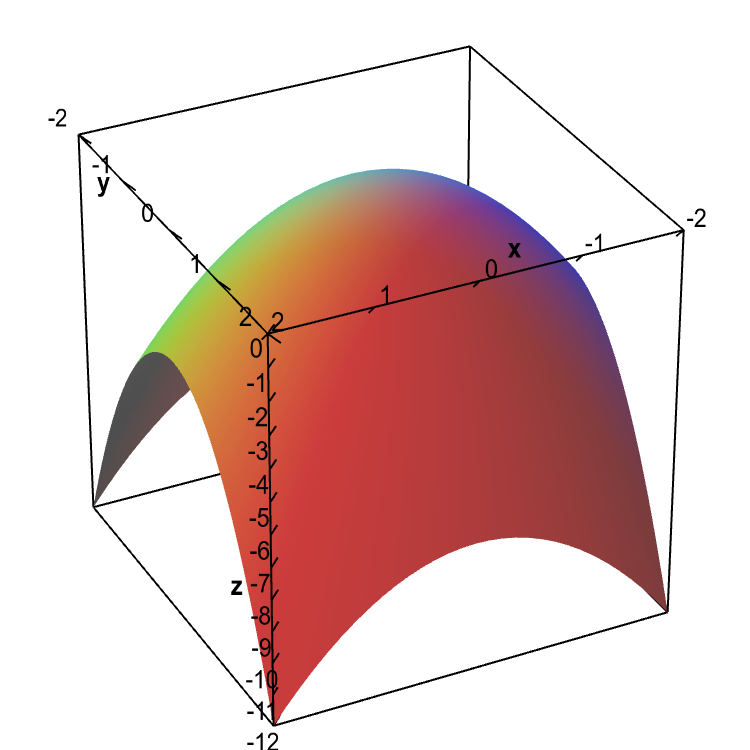



Level Sets Math Insight




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram



1




Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 Study Com




The Paraboloid X 2 Y 2 16 Z Is Intersected By The Ellipsoid X 2 4 Download Scientific Diagram



15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts



Volumen De Un Paraboloide Geogebra




Hallar El Volumen Del Cuerpo Limitado Por El Paraboloide X 2 Y 2 Z 12 Y El Plano Z 8 Brainly Lat




Let S Be Part Of The Paraboloid X2 Y2 That Lies Under The Plane Z Evaluate The Surface Inte Homeworklib




Solved Find And Identify The Traces Of The Quadric Surface X 2 Y 2 Z 1 Answer Transtutors




Multivariable Calculus Surface Area Of Sphere X 2 Y 2 Z 2 16z Within Paraboloid Z X 2 Y 2 Mathematics Stack Exchange



Solved Find The Volume Of The Solid Enclosed By T




Integrales De Flujo Y Teorema De Stoke Terminado Integral Curva




Calc3 1001 By James Bardo Issuu




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram




Volumen Con Integral Doble En Coordenadas Polares Cilindro Y Paraboloide Youtube



Www Ualberta Ca Csproat Homework Math 215 Solution 8 Pdf



Surfaces Part 2
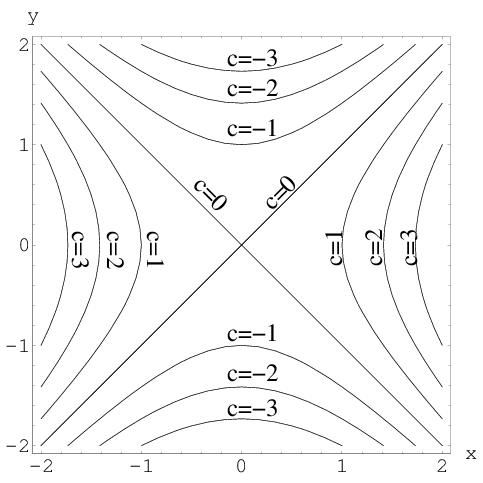



Level Set Examples Math Insight




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange



Mate 17 Calculo Vectorial Taller 2 Preparacion Segundo Parcial P2 A Si F X Y G X Y Son Dos Funciones Continuas En D Entonces Pdf Descargar Libre




Find The Volume Of The Solid That Lies Under The Chegg Com



Www3 Nd Edu Zxu2 Triple Int16 7 Pdf




Find The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Include A Sketch Of The Three Dimensional Paraboloid As



Www Ualberta Ca Rjia Math215 Hwks Sol5 Pdf



23 Match The Equation X 2 Y 2 Z 2 1 With Its Graph Labeled I Viii Toughstem
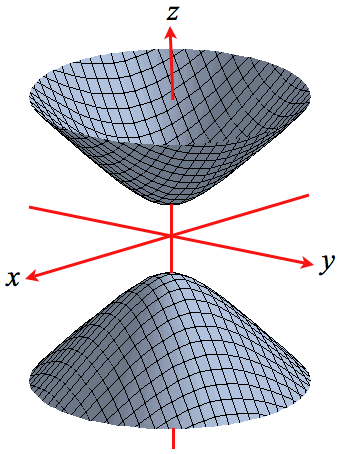



Level Surfaces




1 Consider The Surface Of Paraboloid Z 1 X2 Y2 Chegg Com



Surface Area



1




Find The Volume Of The Solid That Lies Under The Elliptic Paraboloid X2 9 Y2 16 Z 1 And Homeworklib



Http Www Cis Umac Mo Fstitl Calculus12 13 Lecture 07a Pdf




S Consists Of The Paraboloid Y X 2 Z 2 0 Y 1 And The Disk X 2 Z 2 1 Youtube




Integrales Dobles




Answered 4 Let S Be The Portion Of The Bartleby




Slides Show
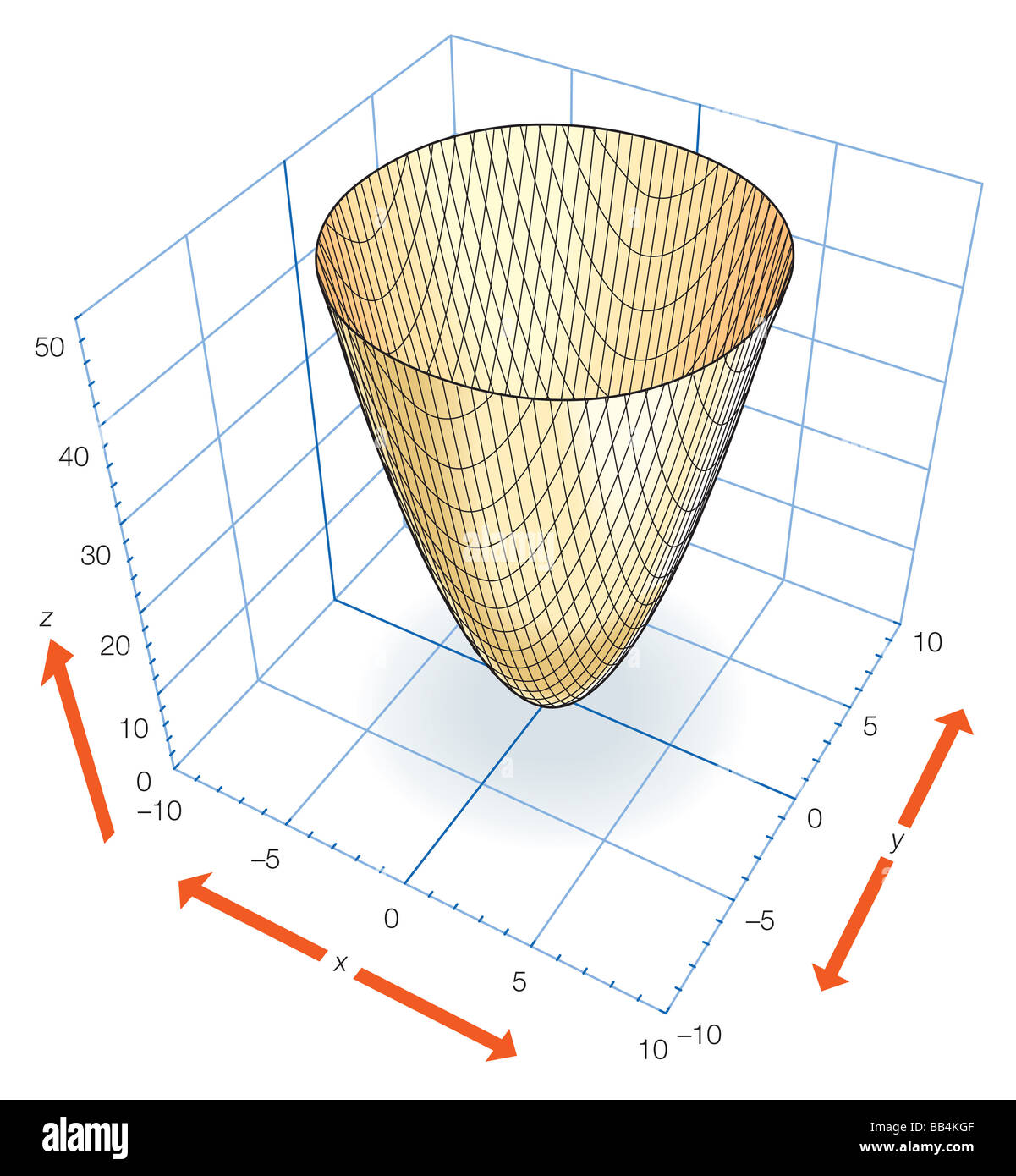



Three Dimensional Parabola High Resolution Stock Photography And Images Alamy



1




Saddle Point Wikipedia
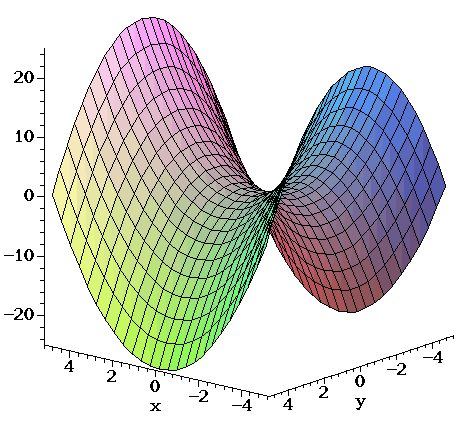



Surfaces Part 2




Int Superficie



Solved 12 1 1 Points Previous Answersscalcet7 143 094 The Paraboloid Z 1 X X2 2y2 Intersects The Plane X 1 In A Parabola Find Course Hero



Calculo Vectorial Guia Unidad5 Cvectorial P44



Find The Surface Area Of The Part Of The Paraboloid Z 5 X 2 Y 2 That Lies Between The Planes Z 0 And Z 1 Mathematics Stack Exchange



23 Match The Equation X 2 Y 2 Z 2 1 With Its Graph Labeled I Viii Toughstem



Surface Area




Find An Equation For The Paraboloid Z 4 X 2 Y 2 In Cylindrical Coordinates Type Theta In Your Answer Study Com




Mat 241 Homework Set 10 Mesa Community College Pages 1 4 Flip Pdf Download Fliphtml5




Stoke S Theorem S Is The Part Of The Paraboloid Z X 2 Y 2 That Lies Insided The Parabaloid And Cyli Youtube




A Hyperbolic Paraboloid Z X 2 Y 2 Download Scientific Diagram




Find The Area Of The Paraboloid Z 1 X 2 Y 2 That Lies In The First Octant Study Com




Evaluate The Volume Bounded By Z 1 X 2 Y 2 And Z 1 Y Mathematics Stack Exchange



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf



What Is The Volume Between Paraboloid Z X 2 Y 2 And Y X 2 Z 2 Quora




Use Polar Coordinates To Find The Volume Of The Given Solid Below The Paraboloid Z 18 2x 2 2y 2 And Above The Xy Plane Homework Help And Answers Slader




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange
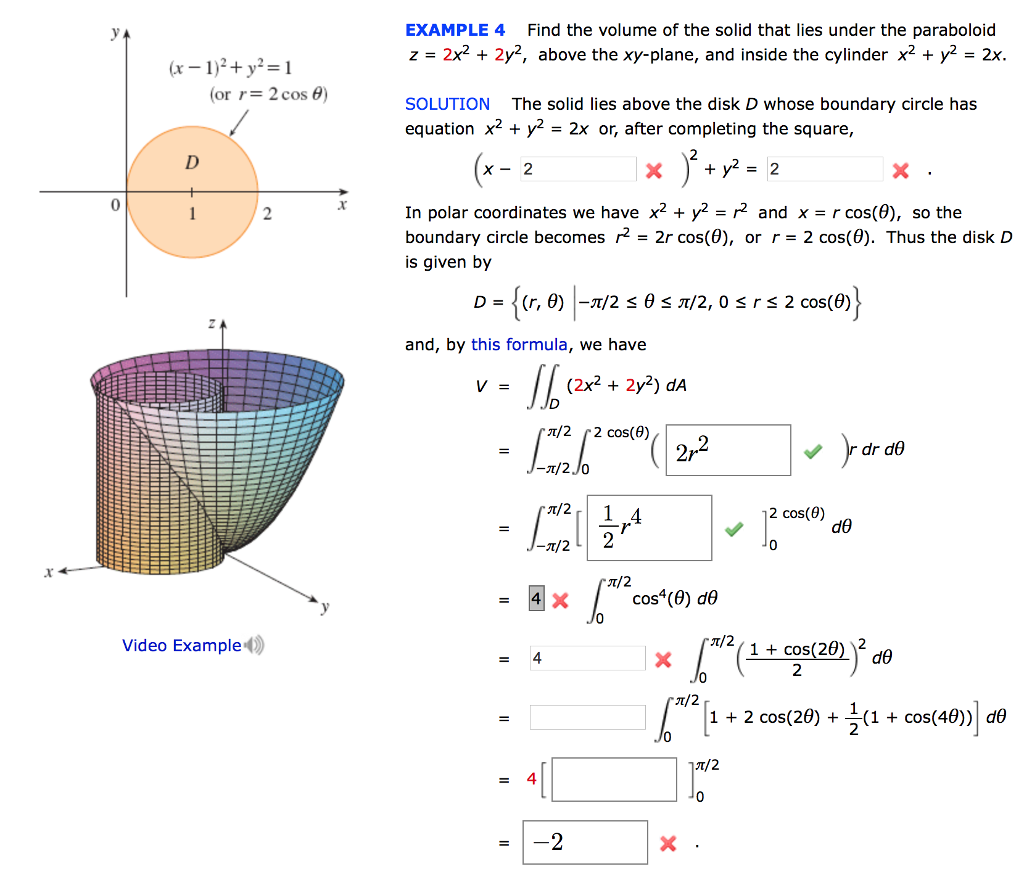



Example 4 Find The Volume Of The Solid That Lies Chegg Com




Calculus Integration Double Integrals 8 Of 9 Example 7 Finding The Volume Paraboloid Youtube




Graph Of Z 1 X 2 Y 2 Novocom Top



Solved Find The Volume Of The Solid Enclosed By T
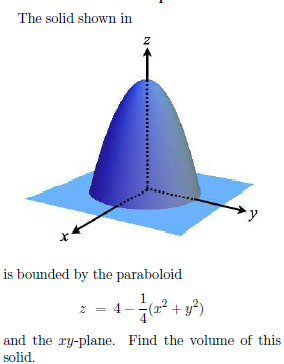



The Solid Shown In Is Bounded By The Paraboloid Z Chegg Com
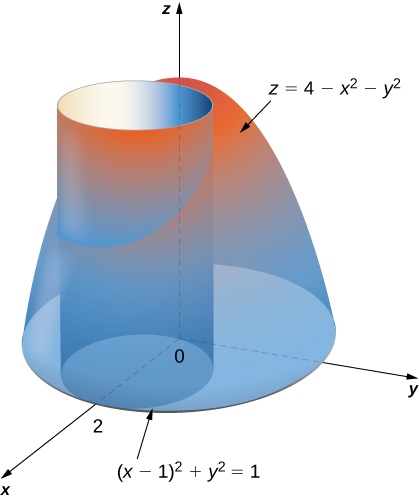



Double Integrals In Polar Coordinates Calculus Volume 3



0 件のコメント:
コメントを投稿